Quick Start

from Inner Algebra How To Do Algebra In Your Head

Previous Chapter ♦ Contents ♦ Next Chapter

Quick Start

We are going to start off with a demonstration. We will take an equation and explain, step by step, how you would solve it mentally. As this happens, you will see many of the techniques and concepts that can be used on other algebra equations. You will be able to apply some of it immediately after reading this chapter.

Here is the equation we will solve.

$\begin{displaymath} 0.5+\frac{4x+3}{2}=1.5+x\end{displaymath}$

Depending on your experience level, this may be challenging, or it could be really easy. In any case, you could solve this by first subtracting 0.5 from each side,

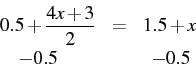
$\begin{eqnarray*} 0.5+\frac{4x+3}{2} & = & 1.5+x\\ -0.5\;\;\;\;\;\;\;\;\; & & \;\;-0.5\end{eqnarray*}$

$\begin{displaymath} \frac{4x+3}{2}=1+x\end{displaymath}$

then multiplying each side by two,

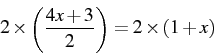
$\begin{displaymath} 2\times\left(\frac{4x+3}{2}\right)=2\times(1+x)\end{displaymath}$

$\begin{displaymath} 4x+3=2+2x\end{displaymath}$

and then collecting the variable by itself on one side.

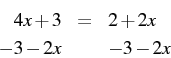
$\begin{eqnarray*} 4x+3 & = & 2+2x\\ -3-2x & & -3-2x\end{eqnarray*}$

$\begin{eqnarray*} 4x+3-3-2x & = & 2+2x-3-2x\end{eqnarray*}$

$\begin{displaymath} 2x=-1\end{displaymath}$

$\begin{displaymath} x=-\frac{1}{2}\end{displaymath}$

Most people would work this out on paper (or a whiteboard or chalkboard), writing some of the steps that were printed above. Math as we know it is primarily visual: equations and symbols are represented as something that can be seen. You read or write an equation, and probably do not hum it or smell it. The methods we have for solving equations reflect this. One such ``tool'' is subtracting a quantity from each side. We used this when we took the starting equation

$\begin{displaymath} 0.5+\frac{4x+3}{2}=1.5+x\end{displaymath}$

and changed it to

$\begin{displaymath} \frac{4x+3}{2}=-0.5+1.5+x\end{displaymath}$

What we are doing is removing a term from one side, in a way that moves us towards the solution, while keeping the equation mathematically correct. We represent this visually - when writing it, or printing it on a page - by printing ``-0.5'' under each side of the equation.

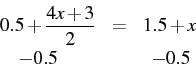
$\begin{eqnarray*} 0.5+\frac{4x+3}{2} & = & 1.5+x\\ -0.5\;\;\;\;\;\;\;\;\; & & \;\;-0.5\end{eqnarray*}$

Let's talk about something else a moment. Like most people, you have certain mental abilities, including a memory, an imagination, and the ability to visualize in your mind's eye. Some people are much better at this than others, but most everyone has some innate skill in these areas. It is also something that people can learn and become better at.

You can use these abilities to solve equations mentally. That, in a nutshell, is what this book is about. I'd like to demonstrate what this means, so I am going to ask you to do something. Please take a moment to close your eyes, and see if you can visualize this equation:

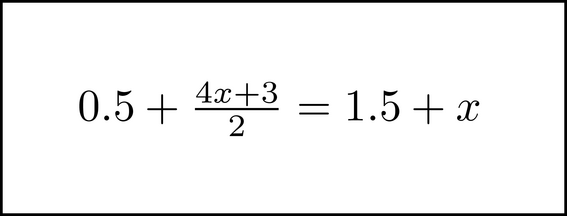
(Well... read the equation first, THEN close your eyes.) Just try it for a few seconds - if it does not come quickly, don't worry about it. You are seeing the equation in your mind's eye. If it is not easy to do, try just visualizing part of it - say, the on the right side. Were you able to do this? This isn't a small equation, so maybe you did not. It's really not important at this point whether you can, because part of what this book does is teach you how to do that. For now, just pretend you have the ability to see equations like this using your imagination - just like an artist can visualize what he will draw before picking up his pen.

If you have the ability to visualize this well, you can do things mentally that you would normally do on paper. To move the 0.5 to the opposite side, you could start by seeing something like this:

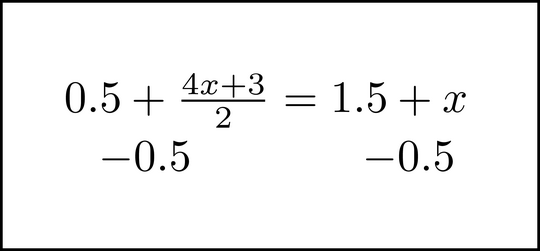
This is similar to what you do if you are working it out on paper, except that you are imagining it rather than writing it. You would then go on to actually do the subtraction, and so on. That's great, but there is something else we could take advantage of here. The procedure above - subtracting a quantity from each side - is presented visually in a certain way. Part of why it is the way it is, is so that it can clearly be represented on paper (or whiteboard, computer screen, etc.) Since we are working within an image that you are visualizing, there are things you can do that could not really be done in any of those mediums. The immediate goal is to take the 0.5 term and remove it from the left side of the equation. Let's see if there is a different way we can accomplish this. Here is the original equation again, below. See it in your mind's eye, if it is easy for you do to so right now. If not, just pretend that is what you are doing as we go along.

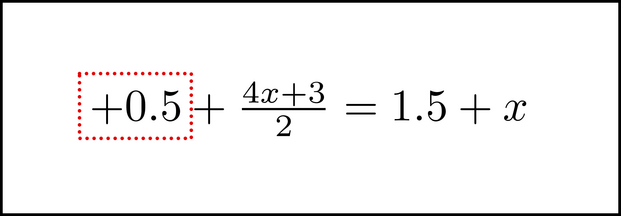
A few things are different here. For one, we have put a plus sign in front of the 0.5. That's fine; it is a positive number anyway, so we are just emphasizing that fact. More unusual is that there is a box of dots surrounding the +0.5. That is a chunk, which is a visual device we use in this book. We say that we have chunked the +0.5. You can chunk a number, variable, expression - any group of symbols in an equation. You chunk an expression when you are getting ready to do something mathematically with it. In this case, we are moving the contents of the chunk to the opposite side of the equation:

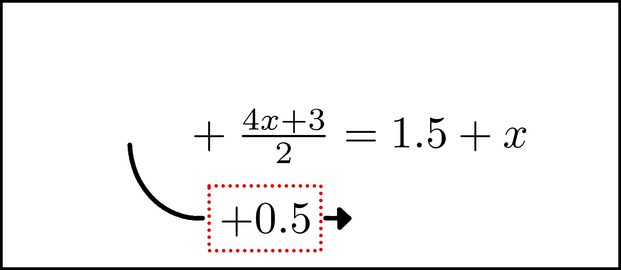
If you are visualizing this equation, ``pick up'' the +0.5 in your image, and begin to move it, just like in the picture here. (If you are just pretending to visualize the equation right now, pretend you are moving the chunk too.) The chunk is like a separate object, that you are taking from its spot on the far left and moving to the right. As you move it, there is something special that you need to do with it. You need to take whatever is inside the chunk and multiply it by -1. Since the number is positive, we just make it negative, like so:

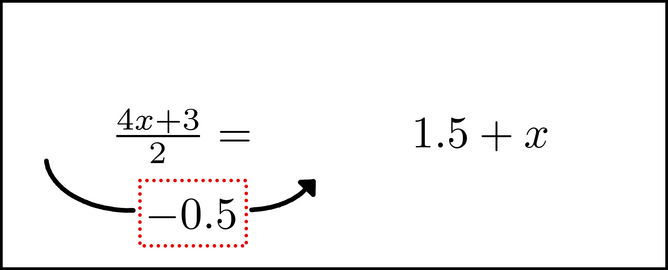
(We've also moved some of the symbols on the right side over, because we are about to insert the chunk there.) Whenever you move a chunk like this, you change the term's sign to its opposite, as if we are multiplying it by -1. If the term was negative - for example, say it was -0.3 inside the dots - we would make it positive (+0.3). The other thing we do here is to remove the + that was between the +0.5 and the $\frac{4x+3}{2}$ when we first started.

The last step is to insert the chunk on the right side of the equation.

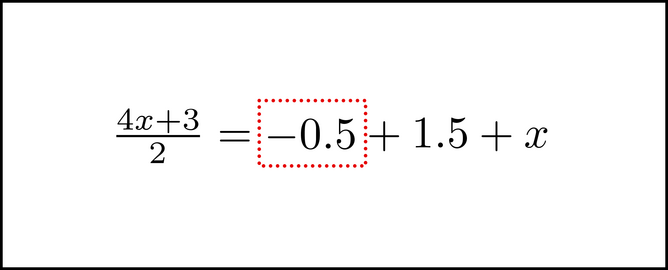
Notice that we are adding it in. We insert the chunk in a way that it is being added to the rest of what is on that side of the equation. We are done with this chunk, so we can remove the dotted box now.

This is an example of symbol motion, which is fully explained in chapter

. Symbol motion involves moving groups of symbols (chunks) in ways that algebraically manipulate the equation. When done correctly, it has the same mathematical effect as the normal methods. The difference is that once you learn to use them, symbol motions are easier and faster to use internally than the techniques used to solve equations by writing them.

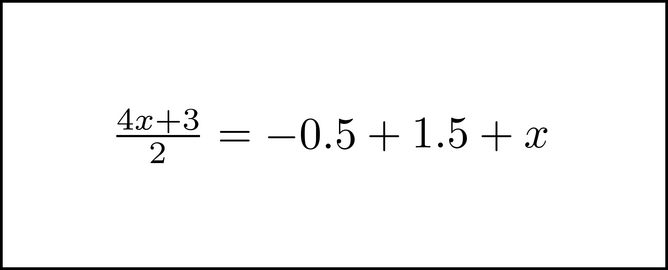
After simplifying the right side a bit, the next step would be to multiply each side of the equation by 2. There is a way to do this with symbol motion also. It starts with chunking the 2 in the left side's denominator.

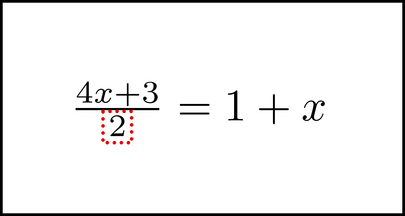
Then we start to move it, like how we did earlier.

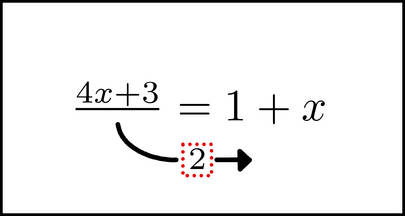
There are several classes of symbol motion. When we moved the 0.5 to the right side earlier, that was one class, in which the effect is similar to adding or subtracting a quantity from each side. When we move the 2 from the denominator, we are using a different class that has an effect similar to multiplying (or dividing) each side by some quantity. Unlike with the ``add/subtract'' class, we do not multiply the contents of the chunk by -1. What we do instead is to move the chunk from the denominator of one side, to the numerator of the opposite side. (Or, if it was in the numerator of one side, we would move it to the other side's denominator.) In other words, if the chunk is on the bottom of one side, we move it to the top of the other side; and if it is on the top of one side, we move it to the bottom of the other side^1.1. We end up with something like this:

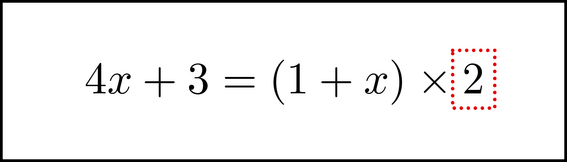
In the process of doing this, a few things in the image have changed again. First, there was a horizontal line in the fraction on the right hand side - now it's gone. Second, we introduced a multiplication sign on the right hand side, between the (which we put in parentheses) and the chunk. Symbols that denote some math operation, like +, -, $\times$ or $\div$ (which is what the horizontal line in a fraction really is), are special. They flit in and out of existence depending on what numbers or variables are present and their relationship with each other.

Let's finish solving this equation. Now that the 2 has been moved, you can dechunk it (remove the dots around it).

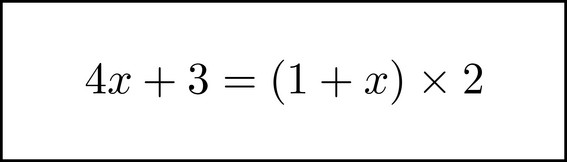
Next, in the visual image you have, you can distribute the multiplication on the right side. This is done just as it would if you were writing the equation out.

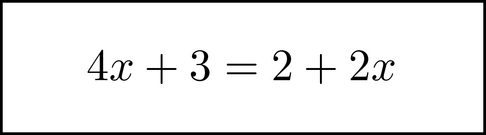
Now we want to collect the variable by itself on one side. Chunk the 2x on the right,

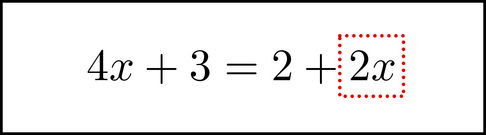
and move it over.

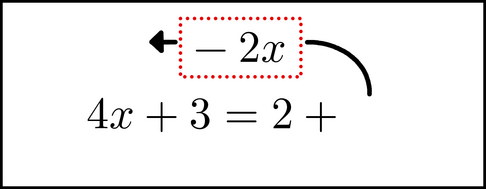
Remember, when you move a chunk like this, you need to flip its sign (which is the same as multiplying it by -1). That it why it is now a -2x instead of 2x. We can actually insert it anywhere in the left side of the equation, just as if we were adding in a term, so let's put it by the 4x.

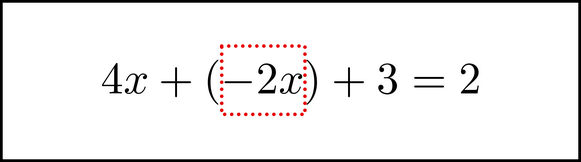
The chunk is put in parentheses here to help make things clear. Since 4x + (-2x) = 4x-2x, when we dechunk the -2x the equation becomes

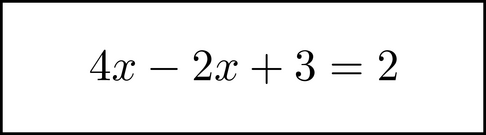
After simplifying, we can move the 3 to the other side of the equation in a similar way to get

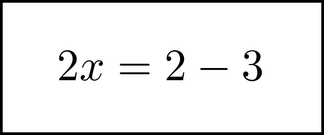
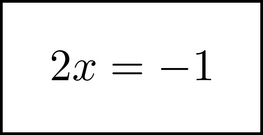
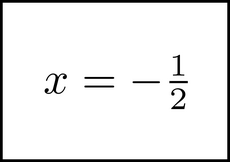
For some of you who are reading this, the equation used above will seem complicated. For others, it will seem simple and maybe boring. The first group will be heartened, and the second group dismayed, to know that this book teaches by using example equations, most of which are simpler than the above. For the second group (and the first group too if you are interested), I want to let you know that although the equations used are ``small'' and simple, everything taught scales to math of almost any complexity. The concepts and tools are introduced using simple equations so that it is clear and obvious how to apply everywhere... including decidedly non-simple equations. The ``challenge'' - the word is in quotes, because it's not really hard - is to take the essence and apply it in new mathematical situations.

There is one last thing to mention. If you encounter an equation that is challenging for you to visualize - and no matter how good you get, there will always be equations that are bigger and badder - you don't have to envision the whole thing at once. There is a technique, called windowing, that lets you visualize only those parts of the equation needed to correctly do the next symbol motion. The practical effect is that you can solve equations that are larger than you can visualize right now. Windowing is detailed in chapter .

Footnotes

... side ^1.1: Keep in mind that any expression can be considered a fraction. Even just 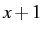can be written as 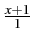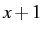$\frac{x+1}{1}$ . is the numerator, and 1 is the denominator.

Previous Chapter ♦ Contents ♦ Next Chapter