Groundwork
Subsections
Groundwork
There are a few key abilities that form a foundation for doing math intuitively. The first is visualization. It is similar to using your imagination. If you have always been a 'visual' person, you will find some things easier. The first part of this chapter helps you develop this ability. If you already feel skilled in this area, this section can help you strengthen it in the specific ways that help you use it for math. Some people are naturally quite good at visualizing. If you feel that you don't really need training in this area, you can skip the first section. Just make sure you can do the exercises at the end of the chapter.
The last section introduces a tool called chunking. Chunking is a way to group (and un-group) symbols and expressions in particular ways that help us solve the equation.
Visualization
Think of a character from a comic, TV show, or computer game that you like. Close your eyes and imagine this character - see them in your mind's eye. Even if it is a fuzzy or incomplete image, that's fine. Just get a definite visual impression of this character.
If you can do that, great! You already have the single most important ability that is necessary to do algebra in your head. You can skip to the next section, ``Visualizing Equations,'' below.
If you could not conjure up this image just now, or you are not sure, don't worry. First, it is not necessary to be able to visualize in any great detail. Let's say the character you picked is a talking duck you liked to watch on TV when you were seven. If you can see just part of the face and bill for a split second, and then it's gone, you can visualize plenty well enough. So just focus on getting that.
Practicing a little goes a long way. Here are some tips:
- Try something. If it works, great. If not, try another approach. What helps one person visualize really well is often different from what will help another person.
- It will probably help to choose a character you have positive feelings about. Think of a small child watching a cartoon, and suddenly a character the child really likes comes on the screen. What does that child feel inside? Avoid characters that kept you awake all night.2.1
- Visualize with your eyes open. Visualize with your eyes closed. Which is more effective for you?
- If it's not easy to visualize the character you picked, pick a different character, or some object that has meaning to you. E.g., if you skateboard, imagine a skateboard, or last year's X Games champ flying on one.
- Find a real picture of the character, or draw one. Look at the picture. Close your eyes, and try to imagine that picture. Repeat. Use the picture as an aid.
- Bring different senses into it. Some people are ``visual'' people; they will usually be able to imagine things in their mind's eye immediately. If you are more of an auditory person, imagine this character talking or making a noise. If you are more of a kinesthetic, ``feeling'' person, imagine the character doing something physically active, and what they would feel while doing it.
- Move the ``physical'' location of the image. When people imagine something, they usually put it in a specific location in the space around or inside them. Some people envision it in front of them, or slightly up or to one side. It can also be located inside your body, such as inside your head. Try several locations to find what works best for you.
- Be willing to give it time. Work on it a little, and if it is not easily coming to you, do something else. Try again in a few hours or another day.
Visualizing Equations
Now we are going to try something with this equation:
Since this equation is so simple, you probably know the answer just by looking at it.2.2 How easy or hard it is to solve does not matter - we are going to do something else entirely with it.
Imagine that you have written this equation in big letters and numbers on a 3 by 5 card, like this:
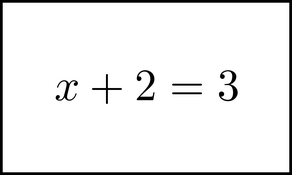
Imagine that this card is floating in front of you, where you can see it. It's at a comfortable distance. You can move it around by imagining it. You want be able to see each individual symbol, 'x', '+', '2', '=' and '3', and their position in space relative to each other. Practice this until you can consistently see the equation on the card. It does not matter if you do it with your eyes open or shut. It can help to write the equation on a real 3x5 card, and glance at it as an aid.
By the way, you certainly do NOT need to discern it in great detail. If, in your imagination, you can recognize each of the five symbols, and get the order right, that's all that is necessary. In other words, as long as YOU can tell that the first symbol is an 'x', even if it does not really look anything like it, that's fine - you are the only one who will ever see it anyway!
Now, take the image and move it around. Move it a few inches left, right, up and down. (Your head is motionless. You are getting practice at controlling where you put the image that you see mentally.) Again, practice this until you can consistently do it.
Now make the image of the equation bigger and smaller. You are zooming in and out. Make it twice its original size. Make it half its original size. Practice until you can do it consistently.
Remember, in all of this, you're not doing anything with the equation, mathematically speaking. You are not taking any steps to solve it. You are merely creating a mental image of it, just like you could imagine a car or a banana or anything. You are then moving that image around while keeping the image more or less intact.
Here is a summary of the steps above:
- Visualize the equation x + 2 = 3 as if it was written on a 3-by-5 card and held in front of you. In your mind's eye, see it in enough detail that you can discern each of the five symbols and their order in the equation.
- Move the image around - left, right, up, down, towards you (in), away (out) - while keeping it whole and clear.
- Zoom in and out. Make the image of the equation half its original size, and twice its original size.
Chunking
This section is about a new verb: chunk. The action of chunking is a key to taking an image you can make in your mind's eye, and using it to solve the equation it represents. You probably have some idea of what it is from chapter ![]() , where it was introduced in the example. It is a tool we use to help rearrange the equation in ways to our liking. Before we can fully define chunking and how we use it, we must discuss a few concepts.
, where it was introduced in the example. It is a tool we use to help rearrange the equation in ways to our liking. Before we can fully define chunking and how we use it, we must discuss a few concepts.
The first concept is the symbol. Math equations are composed of symbols. In the equation x + 2 = 3, one symbol is the variable, 'x'. Two of the symbols represent mathematical processes ('+' and '=' ), and the other two symbols are numbers. They are arranged in a particular order, giving the equation a particular meaning. If you change the order, it may change the meaning of the equation (x + 3 = 2) or it may not (2 + x = 3).
The next concept is an object. What exactly is an 'object'? How do you know something is an object, and how do you know that two objects are distinct? There are things in your environment right now that can be referred to as objects. You are wearing several2.3, and if you are reading this on a computer screen, the display is an object. Anything that you can pick up and move around is an object.
There are also non-physical objects. These are not real in the same sense as tangible objects, but they can still be useful. In particular, and this concerns us, math symbols are objects. Let's look at this equation again:
Each of these five symbols can be considered an object. Whether a particular symbol is on a computer screen, paper, or in your mind's eye, you can consider them the same object.2.4 In other words, the symbol 'x' on a computer screen is the same object as that 'x' on a printed page, and the same as an 'x' you imagine.
What about the equation itself? The equation as a whole is also an object. It is an object that is composed of other objects, the symbols. The same can be said for a jar of pickles, or a box holding kittens. The equation, jar, and box are objects that can hold other objects; when they are put in, the whole thing becomes a new, different, yet related object.
When you look at the equation above, you can focus on one symbol, an expression (group of symbols), or the equation as a whole. Your choice of focus will depend on what you need to do in that moment. When you choose to focus on an expression, or the entire equation, you are taking several objects and treating them as a single whole. This is fundamentally what chunking is. It is about working with an aggregate object that is composed of other objects. It implies a degree of flexibility in your thinking, since you are choosing to focus on an expression (such as x + 2) when it us useful to do so, on the equation as a whole (x + 2 = 3) when that is useful, or on one of the components individually (e.g., just x or 3) when THAT is useful.
Chunking is more about choosing where you put your attention than anything else.
The definition of chunk is ``the action of consciously taking a group of objects, and working with that group as if it is a single object.'' We would say something like ``Chunk the (some group of symbols)''. For example, in the equation
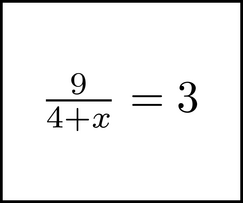
we can say ``Chunk the 4 + x'', which means we are going to work with the expression 4 + x as a group. In this book, chunks are pointed out by drawing a dotted box around them.
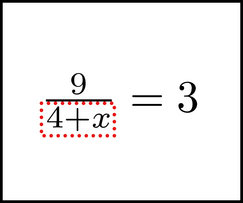
Exercises
Visualization
Pick three algebraic equations that you normally work with, or are similar to equations you typically use. You can choose them from a math textbook if you are a student, or from a research or work project if you are not. Pick equations that you consider to be on the simple side of medium complexity - that is, equations that are complex and 'big' enough to be interesting, but not much bigger. It's also best to pick equations that are fairly different from each other.
When you've chosen them, do these exercises with each equation:
- Visualize the equation as if it was written on a 3-by-5 card and held in front of you. In your mind's eye, see it in enough detail that you can discern each of the symbols and their positions in the equation.
- Move the image around - left, right, up, down, towards you (in), away (out) - while keeping it whole and clear.
Chunking
For each of the following, visualize the equation with the indicated expression chunked. You may first write down the equation with the chunk outlined if it helps you.
- 4x + 3 = x - 7; chunk the x on the right side.
-
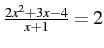 ; chunk the x + 1 in the left side's denominator
; chunk the x + 1 in the left side's denominator -
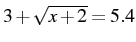 ; chunk the 3 on the left side.
; chunk the 3 on the left side. -
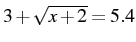 ; chunk the
; chunk the 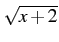 on the left side.
on the left side. -
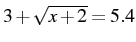 ; chunk the x + 2, inside the square root, on the left side.
; chunk the x + 2, inside the square root, on the left side.
Footnotes
- ...2.1
- If they still keep you up, sorry for reminding you. Better sleep with the lights on tonight.
- ...2.2
- If not, you are reading a book that teaches you how, so don't worry.
- ... several2.3
- Well, you're probably wearing several. I don't know your reading habits.
- ...2.4
- You can also consider them to be different objects. Neither view is more 'correct'. In this book, it is more useful to act as if a symbol like x is the same object regardless of where we see it.