Symbol Motion

Subsections

• Visual Logic
• Movement As Arithmetic
  • Categories of Symbols
  • Addition/Subtraction Class
  • Multiplication/Division Class
  • Combining arithmetic types
  
  
• Summary: The Rules of Symbol Motion
• Exercises

---

Symbol Motion

Let's take a simple equation, 2 + x = 3, and examine the steps in solving it. It would go something like

Notice in particular the first step and the next-to-last step:

There is a pattern here. The 2 is a symbol that is, in effect, moved from the left side of the equation onto the right side. There is a logic to it, which means there are rules to be followed - for one thing, the 2 becomes a -2 as it is moved, in this case. It turns out that there are patterns like this for many algebraic manipulations you might use to solve an equation. By taking symbols, grouping them in particular ways, and moving them according to certain rules, you can solve equations. This is called symbol motion. Doing algebra in this way is not well suited to working equations on paper or a whiteboard. But it is very well suited for solving equations by visualizing them. This chapter explains the patterns of symbol motion, applied to algebra, and how to use them.

Visual Logic

This expression

and this expression

are the same. You probably learned this by memorizing a rule, called the commutative property, which states that the sum of several terms is the same regardless of their order. Because the rule is so simple, most people instantly know that the two expressions are equivalent, and can swap one for the other without much thought.

There is a way this process can be modelled visually. Start with this expression:

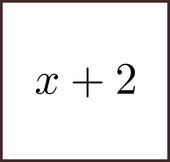
Visualize it, so that you see it mentally. In your image, chunk the x and the 2 separately.

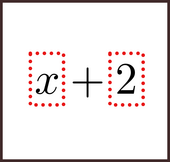
Now, rotate them around the + sign.

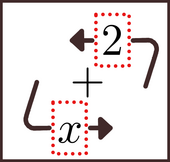
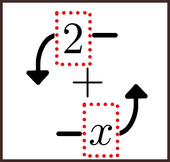
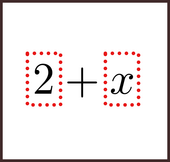
While we rotated it counter-clockwise around the +, there are other possibilities. You can rotate it the other way, or in the third dimension by having one symbol pass in front and the other pass behind. They can even 'teleport', immediately swapping places with each other. Try these out right now. Notice which one seems more natural for you.

The conversion above is a hint of something: we can take an image that has mathematical meaning, and by doing certain graphic manipulations on the image itself, end with the expression in a different, equivalent form. Done correctly, the graphic manipulations have the same effect as normal mathematical methods. Visual logic has to do with the abstract pattern of the change in the image. If the expression above was y + 3, we would transform it to 3 + y, by shifting things around in a similar way to what we did above. Even though the symbols in that expression are different, the visual logic of the transformation would be the same.

When we do a transformation on an equation's image like this, there are two things going on at once. There is the visual logic, the pattern of change in the image itself. There is also the mathematical logic; x + 2 really does equal 2 + x. A pattern of visual logic is really only useful to us if it completely honors the mathematical logic that is represented. As techniques are presented in this and the following chapters, keep in mind that this connection between the visual and mathematical logic has to be maintained in everything we do.

Movement As Arithmetic

If you solve this equation,

you might multiply each side by three,

then add seven to each side,

and finish by dividing each side by two:

These three arithmetic operations can be modelled in a particular, visual manner. When done correctly, they have the same mathematical effect as the ``normal'' way. Let's examine each operation in detail.

Categories of Symbols

Let's examine one of the intermediate equations above:

There are two kinds of symbols here.

1. Quantities. A quantity is a number or a variable that represents a number. 2, x, 7, and 15 are all quantities.
2. Operations, which are symbols that represent a mathematical operation. The only one in this expression is +; symbols like -, 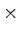(for multiplication), and 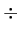are also in this category.^3.1

Operations have an interesting property: they need quantities in order to exist. We can have expressions like

but not expressions like

If the 9 is ``taken away'' because, say, we subtract 9 from both sides of an equation, the expression simply becomes 4x.

Symbol motions can be classified as being in the addition/subtraction class or the multiplication/division class. The classes are named this way because of what their symbol motions do to the equation. Symbol motions in the addition/subtraction class have the same effect on an equation as if you add or subtract a term from each side; and those in the multiplication/division class have the same effect as if you multiplied or divided each side by something. Symbol motions within each category are very similar to each other. Let's look each class in detail.

Addition/Subtraction Class

In the second step, the equation goes from

to

This suggests a pattern of moving symbols, which has the same effect as the normal method of adding 7 to each side. The visual logic is

1. The -7 is moved from one side of the equation to the opposite side, and
2. its sign is flipped - that is, changed to its opposite. It goes from -7 to +7.

Let's see how you can apply this pattern, using symbol motion. Visualize this equation, like you practiced before:

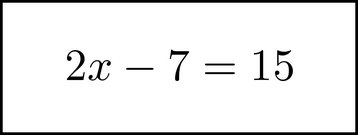
Next, chunk the -7 - put your attention on the '-7' as a separate object, floating in the containing equation.

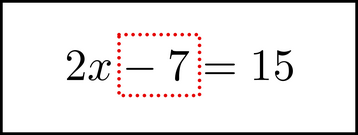
Notice that we are taking two symbols here, the - and the 7, and grouping them together in a single chunk. Next, move that chunk:

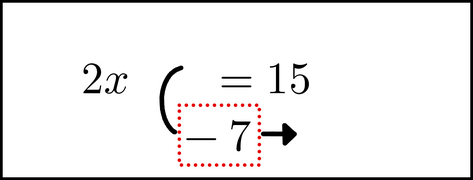
While the -7 is in motion, flip (change) its sign:

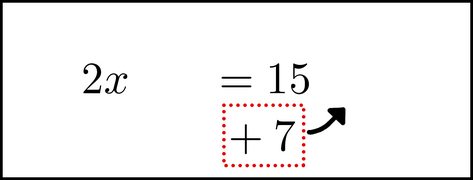
When the motion completes, so does the arithmetic operation:

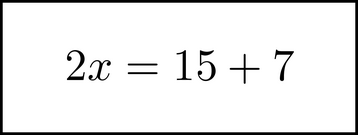
Here is a summary of what we just did:

1. Visualize the equation.
2. Chunk the term (symbol or symbols) you wish to move, including the + or - in front of it. (If there is no + or - there, insert a + in front of it.)
3. In the image you are visualizing, begin to move the chunk to the opposite side. As you do this, flip the sign inside of the chunk. If it has a + in front, replace that with a -, and vice versa.
4. Move the chunk into the opposite side of the equation. Tack it onto the far right. (You can also add it in between other terms that are being added or subtracted. If you put it on the far left, place a + sign between it and the next term.)

You can verify that you moved the symbols correctly, by doing the equivalent operation the ``normal'' way - by adding or subtracting an expression on each side - and check whether the answer is the same.

Multiplication/Division Class

The visual logic for the multiplication/division class is simpler than that for the addition/ subtraction class. Again, we will show how it is done with an example. In the steps at the beginning of this chapter, we go from

in the first step, to

in the second step. First, visualize the equation:

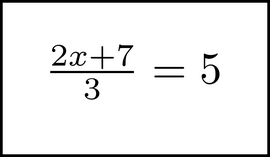
Then, chunk the 3 like this:

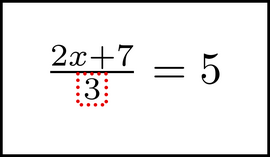
Start to move the chunk to the other side.

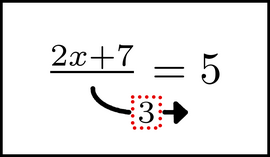
As you can see, the first steps are the same: visualize the equation, chunk a symbol or expression, and start to move the chunk to the opposite side of the equation. The next steps are slightly different. When we move chunks in this way - meaning, in a way that is equivalent to multiplying both sides of the equation by that symbol - we are going to move it from the denominator or the bottom of one side, to the numerator or top of the other side. (By the way, it works the other way too. If we are moving a chunk that starts in the numerator of one side, we would move it to the denominator of the other side.)

What happens when the other side is not a fraction? Actually, it is. In this example, the right hand side is just 5. It is also the fraction . Keep in mind that every expression is also a fraction in this way.

As we move the 3, we do two special things. First, we remove the horizontal line that used to be between ``2x + 7'' and ``3'':

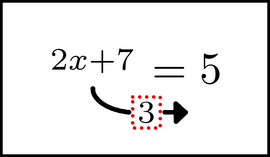
In this image, the horizontal line is a symbol. In particular, it is an operation, in the sense described on page . Remember that an operation needs two quantities in order to exist. When we take one of those quantities away, the operation symbol vanishes. That is what has happened here.

Next, we insert a symbol (that's ``times'', for multiplication, and not the letter x) to the right of the five:

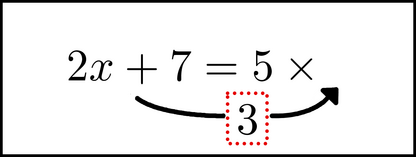
Finally, we move the 3 into place:

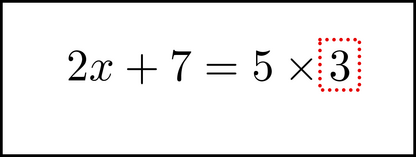
There is another way to do all this. After removing the horizontal line,

we can move the 5 to the right, and put the (multiplication sign) to its left:

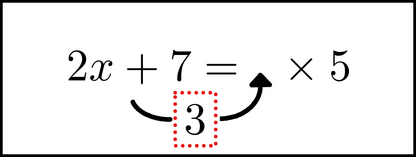
Then we move the 3 into the space to the left of the :

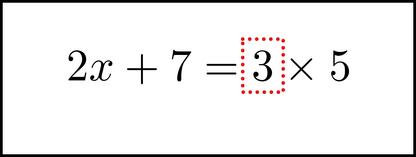
Both ``pathways'' are fine. They are both equivalent to multiplying each side by 3, and that is all that is important.

Division is similar to multiplication. Let's go backwards, from

to

With multiplication, we move the symbol from the denominator on one side to the numerator on the other side. With division, it is the opposite. We are taking a term from the numerator (or just from the expression, if it is not a fraction) on one side, and moving it into the denominator on the other side.

Start by chunking the 3.

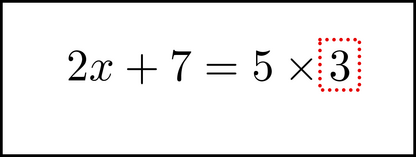
Begin to move the 3 across.

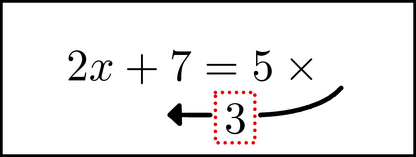
As it moves, we do two things. First, we drop the multiplication symbol (the ) on the right side.

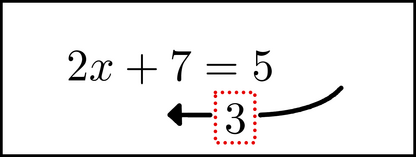
Also, since we are going to make the left side into a fraction, we need to bring in the operator. In other words, we need to draw a horizontal line under the numerator:

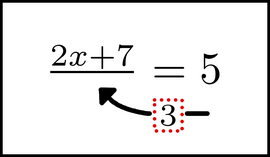
(Note that in this situation, ``bring in the operator'' and ``draw the horizontal line'' are two ways of saying the same thing.) This done, we finish moving the 3 into the denominator of the left side.

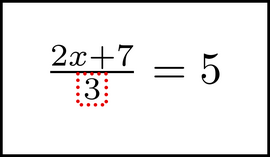
Combining arithmetic types

Here is a more complex example, which is solved with a combination of the above methods. First we will briefly solve it using the normal algebraic methods. Then we'll solve it again using symbol motion. In this equation,

one way to solve it is to first multiply each side by 2:

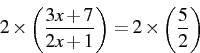
Then, multiply each side by (2x + 1).

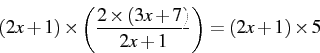
Collect the variables on one side and the numbers on the other, and simplify.

Now, how do we do the same thing through symbol motion? Before we start, it's good to point out a few things. First, when moving symbols, we obey the normal rules of arithmetic. For example, if we are solving this equation:

we would chunk the x + 3

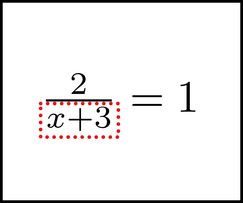
and begin to move it to the right side.

We would certainly NOT do something like this:

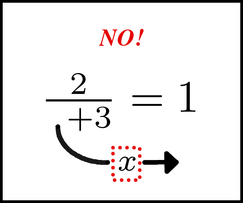
We can always be clear by asking what sequence of arithmetic operations that the symbol motion is supposed to emulate. Here is a general principle:

Every symbol motion has the same effect as a sequence of mathematical operations.

If (and only if) some change in the image is equivalent to some such sequence, is that change a valid symbol motion. If there is no such sequence of operations, the change is not a symbol motion and has no mathematical meaning.

Let's work the equation at the beginning of this section again, this time using symbol motion.

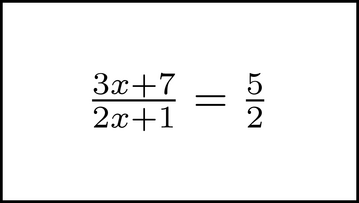
We'll start by making two chunks, both of which will be moved:

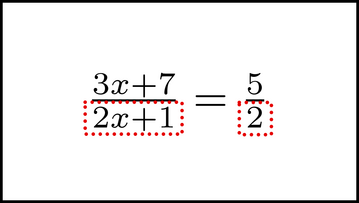
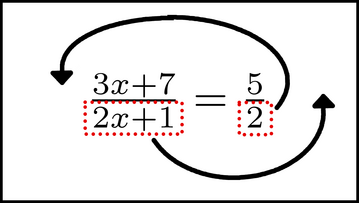
Both of these chunks are in the denominators. We move each of them to the numerator of the opposite side:

As we do this, we erase the horizontal lines, and insert multiplication symbols () as appropriate.

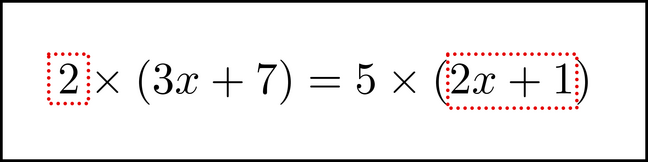
Notice that we have also put parentheses around two of the expressions. This is sometimes needed when symbols are moved around, for the same reason they are needed in normal algebraic manipulation. Next, we distribute the multiplication on each side:

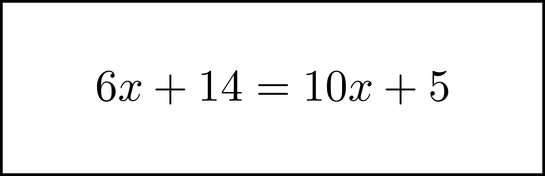
Chunk the 6x and the 5, and begin to move them.

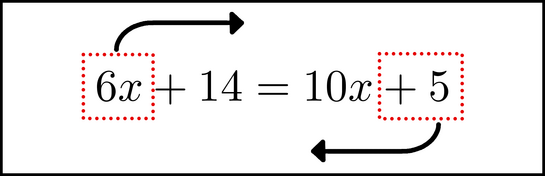
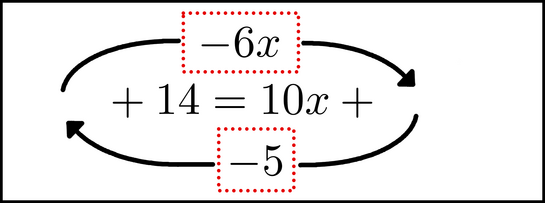
As we do this, we switch the signs of each, from 6x to -6x and 5 to -5.

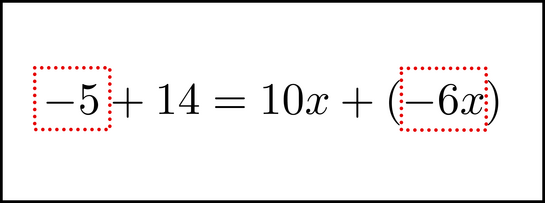
Normal arithmetic quickly solves the rest ( .

Summary: The Rules of Symbol Motion

There are two classes of symbol motions: those that are equivalent to an addition or subtraction operation, and those that are equivalent to a multiplication or division operation.

In the addition/subtraction class, you start by chunking the expression you want to move. If there is a + or a - to the immediate left of the expression, you include that symbol in the chunk. As you move the chunk, you multiply its contents by -1 (i.e., just flip its sign). You normally insert the contents of the chunk at the far right of the opposite side. You can also insert it in another location, if you add it in between terms that are being added or subtracted together.

For the multiplication/division class, start by chunking the expression you wish to move. If it is in the numerator of its current side, you will move it to the denominator of the other side; if it is on the denominator, you move it to the opposite side's numerator. (If one side does not look like a fraction, it actually is - just put it over 1.)

Exercises

Do the following with each equation below:

1. On paper, solve the equation for x using the normal methods, writing down the intermediate steps.
2. Next, also on paper, solve the equation using symbol motion. Outline the chunks, and use arrows to point out what is moving and where. Write (draw) each step in which a symbol is moved.
3. Solve the equation using symbol motion, with your visual imagination - in other words, without writing it down. If you at first need to write down some of the intermediate steps, or use what you wrote in steps 1 and 2 as a guide, you can do so. Just make sure to use that to support your learning, not to ``cheat''. Repeat the process until you are able to solve the equation mentally without those aids.

Here are the equations:

1. 2x + 3 = 7
2. 
3. 
4. 
5. 

---

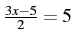
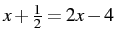
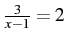
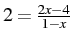
Footnotes

...^3.1

The equal sign would be in a third category, called relations. For now, we are just concerned with the first two categories.

---

Copyright 2005-2010 Aaron Maxwell. All rights reserved.