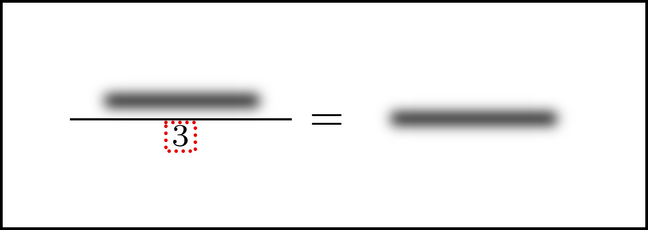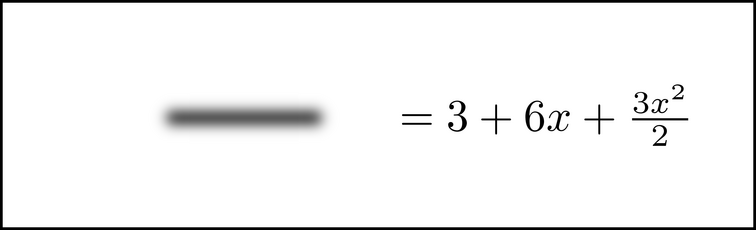Some Advanced Techniques

from Inner Algebra How To Do Algebra In Your Head
Previous Chapter ♦ Contents ♦ Next Chapter


Subsections


Some Advanced Techniques

Having been introduced to the basics, there are two techniques you can learn now. The first is called windowing, and has been mentioned briefly in chapter [*]. It is a tool that helps you work with images faster, and work with equations that are larger than you can easily visualize. The second technique is called correspondence. You will use this simple concept and skill when solving quadratic equations, using expressions with exponents and logs, and other situations.


Windowing

You now have some experience visualizing equations, and working with those images. This is important. As you can tell by now, pretty much everything you learn to do in this book starts with seeing math symbols in your mind's eye.

If you needed to envision the whole equation completely in order to solve it, you could sometimes run into trouble. What if you want to solve an equation that is just too big for you to visualize at this point? Even when you have more practice and become very good at visualizing - or if you are naturally talented at it - bigger and more complex equations will always exist.

Fortunately, you can sidestep all this using a technique called windowing. To use windowing, you do need to be able to remember the equation. The rule of thumb is that you will need to remember it well enough that you could write it down (though you normally would not). At the same time, you would only have to be able to visualize a portion of it at once. Note we are making a distinction between two mental capacities you have: your memory, and your ability to visualize. Most people will find they can exactly remember equations that are much larger than the biggest one they can visualize. Using this ability, you can mentally see enough of the equation to begin processing it.

For equations you can visualize easily enough, you may still want to use windowing, because doing so will let you solve the equation faster and more easily. I actually use windowing for almost every equation I solve mentally, except for very small ones.

What portion of the image (equation) do you need to be able to visualize? It depends. As you have learned, you solve the equations by manipulating the image in particular ways. Normally you are only changing part of the image at any one time. You apply windowing by visualizing those parts of the equation that need to be manipulated, applying the operations to them, and then translating the effect back into your memory of the equation. The key is to become flexible at calling up an image of those parts when you need them. For example, pretend you are solving this equation.


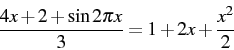
\begin{displaymath} \frac{4x+2+\sin2\pi x}{3}=1+2x+\frac{x^{2}}{2}\end{displaymath}

Perhaps you can visualize this whole equation, perhaps not. Let's see how the use of windowing can help us solve this equation without visualizing every bit of it. The next obvious step in solving it is to multiply each side by 3. The way to do this is to visualize the equation, and chunk the 3 on the left side's denominator.

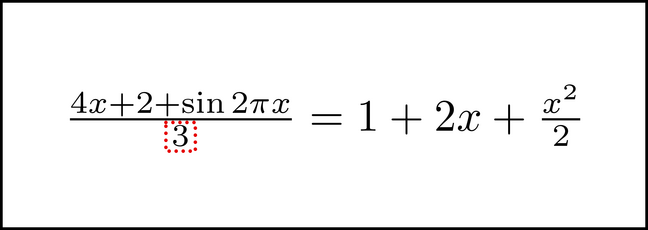
Image fig_window_Ab

Then, you would move the chunk to the other side like this:

Image fig_window_Ac

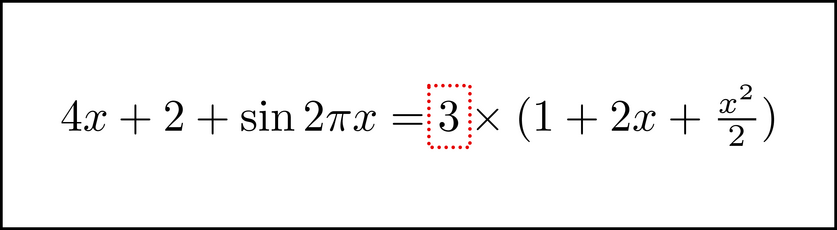
Image fig_window_Ad

The thing to notice is that only part of the image (the 3 in the left side's denominator) moved. Most of the image did not change at all. Whenever this happens, we have a ripe opportunity to use windowing. See if you can visualize this:

Image fig_window_Ae

Those are just blurs where the $4x+2+\sin2\pi x$ and $1+2x+\frac{x^{2}}{2}+x^{4}$ used to be. A lot easier to visualize, isn't it? The essence of windowing is to choose to visualize portions of the equation - in this case, the chunked 3 and a few symbols that show the equation's structure - and purposefully allowing the rest of the equation to be foggy. You can visualize those fogged-out parts later, if and when you need them.

You don't have to imagine blurry bars there, by the way - you can visualize squiggly purple lines, empty space, or something else. Experiment, and do what works best for you.

You can move the chunk just like we did a few images ago:

Image fig_window_Af

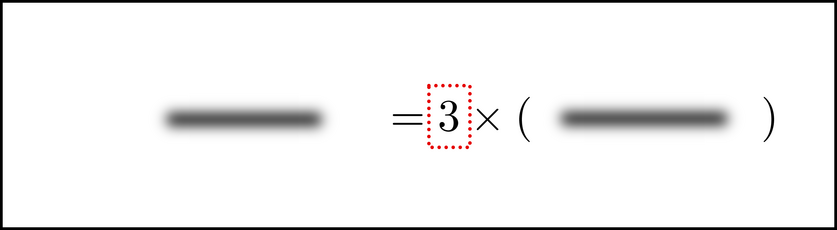
Image fig_window_Ag

You then ``bring in'' the other symbols as needed. That is, when you are ready to use them, you can take parts of the equation that are foggy and fully visualize them. Since a good next step is to distribute the multiplication on the right hand side, we can bring the symbols that are in the parentheses in next.

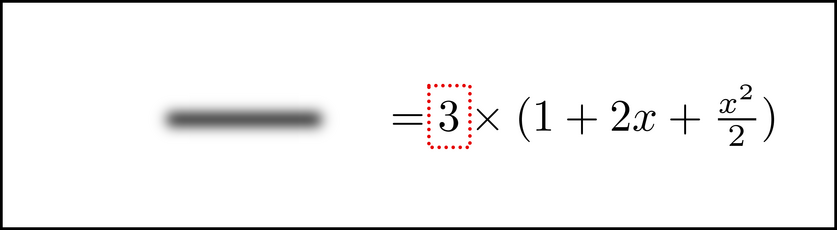
Image fig_window_Ah

Then you can de-chunk the 3 and multiply out the right side like normal.

Image fig_window_Ai

Alternatively, you can un-blur each of the three terms - 1, 2x, and $\frac{x^{2}}{2}$ - one at a time, multiplying each term by 3 before getting the next.

Windowing is very natural once you get used to it. In fact, you may already have started doing it before reading this chapter, perhaps without realizing it. If you are not at that point yet after working this chapter's exercises, you can get there by introducing it gradually. When you solve equations using symbol motion, visualize the whole equation at first if you need to. Notice if there are parts of the equation you are able to not visualize, even briefly. You can bring those parts back ``in focus'' when they are needed to further solve the equation.

Correspondence

What you have learned so far has all involved taking an equation's image and making incremental changes or manipulations to it. There are instances, however, in which you will need to make some wholesale change to the entire equation. A good example is in solving certain equations containing logarithms, such as this one.


\begin{displaymath} 3\log(x+1)=6\end{displaymath}

(This is a base 10 logarithm.) Using symbol motion would get you here:


\begin{displaymath} \log(x+1)=2\end{displaymath}

To go further, you would need to use the property that states that $\log_{b}a=c$ means $b^{c}=a$. Correspondence is when you construct a new image, based on information such as this, that contains the equation in a different form. In this case, you would first have an image like this,

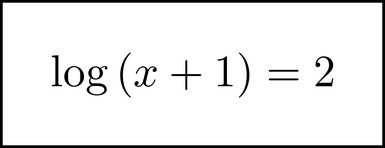
Image fig_tech_a

and substitute it with an image like this,

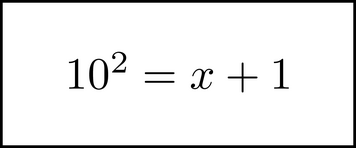
Image fig_tech_b

which you can use normal arithmetic and symbol motion to solve. Another example of this process is when you use the quadratic formula to solve an equation.

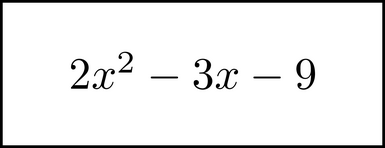
Image fig_tech_c

You would substitute that image with this one.

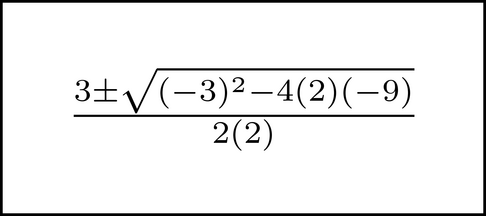
Image fig_tech_d

This is nothing new - everyone learns to do things like this in their first or second algebra course. What is new is that you are doing this kind of equation-wide substitution mentally. You are applying it to the representation of the equation you have in your mind's eye. It may take practice before you can do it well (though it's also possible it will happen for you immediately). It is a simple process, and by the time you have some experience at doing this, it will be second nature.

Exercises

Windowing

Choose three equations that are big enough that you can remember (meaning you can write them down by memory) but are bigger than you can easily visualize. (If you can visualize all equations you can remember, just choose three of the largest equations you can visualize.) You will get the most out of this exercise if you pick equations that are fairly different from each other. Write down these equations so that you can refer to them. You will also need another blank sheet to write on.

Do the following with each equation.

  1. Look at the equation, and study it so that you can remember it. Turn over the sheet or cover it, so you can't see it. On your other sheet, write down that equation from memory. When you are done, check that you remembered it 100% correctly - that's important! If what you wrote down does not match, or you are not able to remember it, study it again and repeat until you are able to do this.
  2. Where you wrote down the equation, divide it up into three to five expressions, circling each one. You want to choose expressions that you are able to visualize (since that is what you will be doing with them). When you are done, every quantity in the equation should be in a circled group. For example, if your equation is 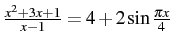$\frac{x^{2}+3x+1}{x-1}=4+2\sin\frac{\pi x}{4}$, you might circle the x - 1 on the bottom left, the 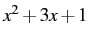$x^{2}+3x+1$ on the top left, the 4 on the right, and the 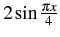$2\sin\frac{\pi x}{4}$, for a total of four circled expressions. (You don't necessarily need to circle all the operators.)
  3. Cover the equation so that you can't see it (or close your eyes, etc.) Visualize the structure of the equation, like in the figures on pages [*] to [*], so that you are able to see its general outline (even if you are not visualizing each and every symbol involved). Include in the image one of the expressions you circled before. You will end up visualizing something that has the general structure of the full equation, with the circled expression visualized and the remaining symbols blurry or just not visualized. Practice if you need to, until you can mentally see this. You can write/draw a diagram (like the figures mentioned above) to help you if needed.
  4. Next, allow that circled expression to fade out. Pick one of the other circled expressions, and bring it into the image instead. You are doing something exactly like in the previous step, just with a different circled expression. Practice if needed, until you are able to mentally see this. Repeat this process with each remaining circled expression.

Correspondence

  1. Take each of these equations, and using symbol motion, reduce them to the form 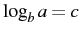$\log_{b}a=c$. Then visualize them in the converted form, 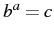$b^{a}=c$, and finish solving the equation from there. (For example, take the equation 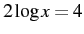$2\log x=4$. First you simplify it to 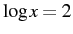$\log x=2$, using symbol motion. Then you visualize it in its converted form, 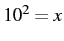$10^{2}=x$, or x = 100.

    1. $3\log(x+1)=3$
    2. $-2+\ln x=4$
    3. $3+2\log(2x+20)=7$
  2. Find the root of each quadratic equation below. (Since we haven't covered how to deal with multiple solutions yet, just find the more positive root, 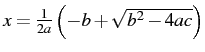$x=\frac{1}{2a}\left(-b+\sqrt{b^{2}-4ac}\right)$.) Solve it by rearranging the equation to the form 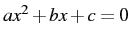$ax^{2}+bx+c=0$, using that to construct the equation for the more positive root above, then solving from there. Do all of this mentally, using symbol motion, correspondence, etc. For example, if the equation is 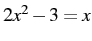$2x^{2}-3=x$, you will visualize it, use symbol motion to change it to 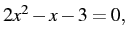$2x^{2}-x-3=0,$ then convert that to

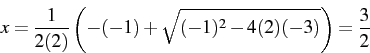
    \begin{displaymath} x=\frac{1}{2(2)}\left(-(-1)+\sqrt{(-1)^{2}-4(2)(-3)}\right)=\frac{3}{2}\end{displaymath}

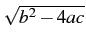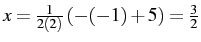    Since visualizing that whole expression may be tricky, you can visualize and solve just $\sqrt{b^{2}-4ac}$ first. Then visualizing the rest is easier: $x=\frac{1}{2(2)}\left(-(-1)+5\right)=\frac{3}{2}$.

    1. $x^{2}+2x-3=0$
    2. $-x^{2}-4x=3$
    3. $6x-5=x^{2}$
    4. $-2x^{2}-8x=6$
Solutions: 1(a) x = 9, (b) $x=e^{6}$, (c) x = 40. 2(a) x = 1, (b) x = -3, (c) x = 1, (d) x = -3




Previous Chapter ♦ Contents ♦ Next Chapter